Binomial Distribution of Allele Data

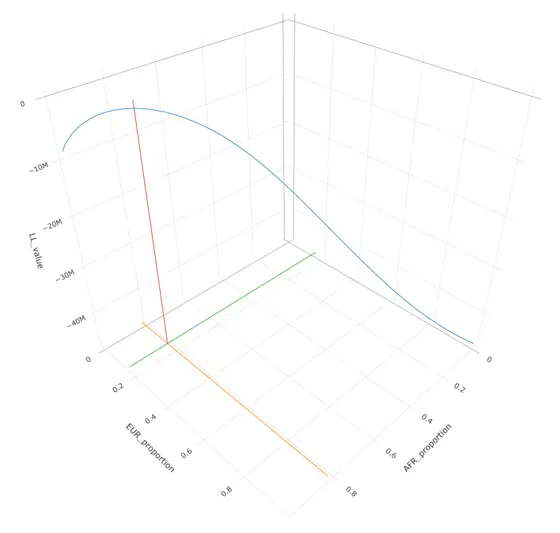
Summary population allele data can be modeled using a binomial mixture distribtion with homogeneous reference populations. Here we show an example of this using the gnomAD V2.1 African/African-American data set, and homogeneous African and European reference panels from 1000 Genomes. We adopt the following model:

where

S is the set of SNPs

K are ancestries

${\pi }_k$ are ancestry proportions for k

$n_i$ is the Allele Count for that SNP

$N_i$ is the Allele Number for that SNP

${\theta }_k$ is the Allele Frequency for that SNP

This leads to the above image which shows a maximation of the log likelihood at the following values:

AFR: 0.8277273 EUR: 0.1722727

These values are consistent with known admixture within the gnomAD sample, and are confirmed with other estimation methods (Summix, ADMIXTURE). There are several ways to maximize the log-likelihood including grid-search and Expecation-Maximization algorithms. The binomial distribution can also be inverted and solved using gradient descent methods, such as Sequential Quadratic Programming.